Nowadays, we study various types of shapes which is useful in day to day life. These shapes are used in building elevation, flooring, fashion designing, and various arts.
In this article, we are discussing triangle and it's various topics.
Here is the content of our mini-guide on the triangle which will help you as a beginner.
So first we start with the definition of a triangle and discuss parts of a triangle.
1. What is a triangle?
Triangle is a simple closed shape which is made only from three line segments.
Or
Triangle is a polygon of three sides.
Or
Triangle is a simple closed shape with three vertices.
2. Parts of a triangle
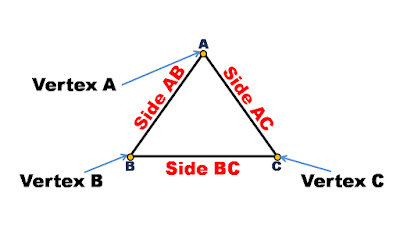
There are various parts of a triangle-
Side
A side is a line segment by which we make a triangle.
Vertex
Vertex is a point where two sides join together.
Angle
An angle is an exposer between two sides.
Interior Angle
An angle that is inside the triangle is known as an interior angle.
Exterior Angle
An angle that is outside the triangle is known as an exterior angle.
Median
Median is a line segment that divides a triangle into two equal parts.
Height
Height is a perpendicular line segment that shows the elevation of a triangle.
Sometimes median and height are same in a triangle.
Triangle has three sides, three vertices, three interior angles.
We explained triangles & components of triangles now we need to explain the types of triangles.
3. Types of triangles
There are various types of triangles. Triangles may be classified based on their sides & angles.
First, we discuss types of triangles based on their sides.
Types of triangles based on sides-
Equilateral triangle
Triangle whose all sides and angles are equal (60°) is known as an equilateral triangle.
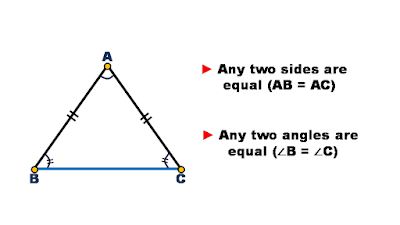
Isosceles triangle
Triangle whose any two sides and any two angles are equal is known as an isosceles triangle.
Scalene triangle
Triangle whose all sides are different in length is known as a scalene triangle.
Types of triangles based on angles-
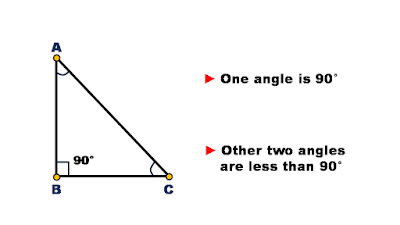
Right-angled triangle
Triangle whose any one angle is 90° and the other two angles are less than 90° is known as a right-angled triangle.
Acute angled triangle
Triangle whose all angles are less than 90° is known as an acute-angled triangle.
Obtuse angled triangle
Triangle whose any one angle is more than 90° and the other two angles are less than 90° is known as an obtuse-angled triangle.
Generally, we learn above all kinds of the triangle.
But when a triangle contains two properties(based on their sides & angles) then we must study the below triangle.
Types of triangles based on both angles and sides-
Acute-angled equilateral triangle
When a triangle contains both properties in which all angles are equal(60°, 60°, 60°) or less than 90° and all sides are equal is known as an acute-angled equilateral triangle.
Right-angled isosceles triangle
When a triangle contains one right angle(90°) and the other two angles(45°, 45°) or sides are equal is known as a right-angled isosceles triangle. This triangle includes 90°, 45°, 45° angles.
Obtuse-angled scalene triangle
When a triangle contains one angle more than 90° and all sides are different in length is known as the obtuse-angled scalene triangle.
Above all these are the classifications of the triangle which we generally study.
Now we are going to talk about the properties of a triangle. By the properties of the triangle, we may solve various problems.
4. Properties of triangle
There are several properties of the triangle which helps to solve the questions.
Let's discuss it one by one-
Pythagoras theorem (Pythagoras property of right triangle)
It states - In a right-angled triangle square of the longest side is equal to the sum of the square of the other two sides.
It means the square of the hypotenuse(H) is equal to the sum of the square of perpendicular(P) and base(B).
H² = P² + B²
When we have given any two sides in the right-angled triangle then we may find the remaining side by Pythagoras theorem.
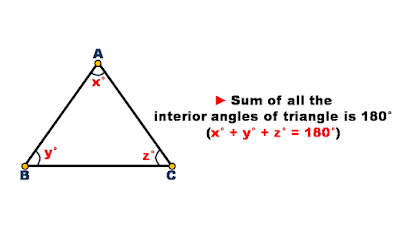
Angle sum property of triangle
It states - Sum of all the interior angles of the triangle gives sum 180°.
∠A + ∠B + ∠C = 180°
When we have any two interior angles in a triangle and we want to find the remaining interior angle of a triangle then we may use this property.
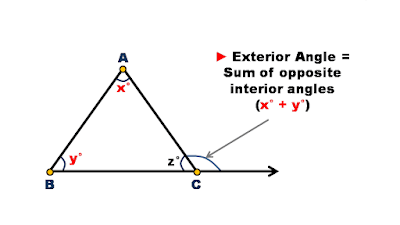
Exterior angle property of triangle
It states - Exterior angle of a triangle is equal to the sum of its opposite interior angles.
x° + y° = Exterior angle
Sum of two sides of the triangle
It states the sum of any two sides of a triangle is always greater than its third side.
By the above property, we can find any exterior angle of the triangle.
And we know exterior angle so we may find interior angles.
Now it's turn to know about the area of triangle.
5. Area of triangle
Area of triangle is the region surrounded by sides of a triangle.
We have several formulas to find the area of a triangle. Let's discuss-
Area of a right-angled triangle(Right triangle)
ar∆ = 1/2×Base×Height
This formula is very useful if we have a base and height of any right triangle.
Area of an equilateral triangle
ar∆ = √3/4×side²
Heron's Formula
Heron's formula helps to find the area of all types of triangles. If we know all the sides of the triangle.
ar∆ = √{s(s-a)(s-b)(s-c)}
Where,
s(semi-perimeter) = (a+b+c)/2
a, b and c = sides of the triangle.
6. Perimeter of triangle
The perimeter of a triangle is the length of its boundary.
The formula for the perimeter of a triangle = The sum of the length of all sides.
Or
3×side of a triangle (for equilateral triangle)
By the above formulas, we may find the perimeter and any unknown sides of the triangle.
7. Congruence of a triangle
When all sides and angles of a triangle are equal to the corresponding sides and angles of another triangle then both triangles are congruent to each other.
There are various rules for the congruence of the triangle-
SSS congruence rule (Side-Side-Side)
If all sides of a triangle are equal to the corresponding sides of another triangle then both triangles are congruent by the Side-Side-Side (SSS) congruence rule.
ASA congruence rule (Angle-Side-Angle)
When any two angles and a side of a triangle are equal to the corresponding angles and side of another triangle so both the triangles are congruent by the Angle-Side-Angle (ASA) congruence rule.
SAS congruence rule (Side-Angle-Side)
When any two sides and an angle of a triangle are equal to the corresponding sides and angle of another triangle so both the triangles are congruent by the Side-Angle-Side (SAS) congruence rule.
RHS congruence rule (Right angle-Hypotenuse-Side)
When one side and hypotenuse of a right-angled triangle are equal to the corresponding side and hypotenuse of another right-angled triangle then both the triangles are congruent by Right Angle-Hypotenuse-Side (RHS) congruence rule.
8. Similarity of a triangle
When the corresponding sides of two triangles are in proportion or equal and corresponding angles are equal then they are similar to each other.
Questions / Answers
1.) How triangle are congruent?
When any two triangles satisfy SSS, SAS, ASA and RHS congruence rule then both triangles are congruent to each other.
2.) How triangles are similar?
When all interior angles of two triangles are equal and their corresponding sides are in proportion so they are similar to each other.
3.) What triangle is both scalene and right?
Triangle whose all sides are different in length and anyone interior angle is 90°. So it will be both a scalene and right triangle.
4.) Which triangle is a 30°-60°-90° triangle?
A right-angled triangle is known as 30°-60°-90° triangle because it has one angle is 90° and the other two angles are less than 90°.
5.) Which triangle is both scalene and acute?
Triangle whose all sides are different in length and all angles are less than 90°. So it will be both a scalene and acute triangle.
Finally, we completed our mini-guide on the triangle which covers the introduction of triangle, properties.
Please comment us for any query related to this article....
