How to find the area of sector & segment of a circle?

UTPAL SHARMA

In mathematics, we learn how to find the area of a circle. In this blog, we will discuss what is a sector, segment, chord & how to find the area of a sector & segment of a circle.


Sector, Segment & Chord of a Circle?

Radius:-

It is a fixed-length from the centre to the boundary of a circle. It is always constant for a circle. As shown below OA & OB.

Diameter:-

It is twice of a radius. It always passes through the centre of the circle. Diameter = 2×Radius.

Chord:-

It is a straight line in a circle which touches the boundary of the circle from both sides. As shown below PQ.

The diameter is the longest chord of any circle.

How to find the area of sector & segment of a circle?

Sector:-

It is a region of a circle which is enclosed between two radii & an arc of a circle. As shown above. It may be classified as-
  • Minor sector- It covers less area between two radii & an arc of a circle.
  • Major sector- It covers more area between two radii & an arc of a circle.

Segment:-

It is a region between an arc & a chord of a circle. As shown above. It may be classified as-
  • Minor segment- It covers less area between a chord & an arc of a circle.
  • Major segment- It covers more area between a chord & an arc of a circle.


How to find the area of Sector?

For finding the area of a sector of a circle we have a formula-
Area of sector = (θ/360º)×Ï€r²
Where
  • θ=Angle of minor sector or major sector.
  • Ï€=22/7 or 3.14
  • r=radius of circle
For better understanding, we take an example. Let's discuss-

Question:-

Find the area of the sector with radius 5 cm & if the angle of the sector is 80º.

Answer:-

First, we draw an image for better understanding.

How to find the area of sector & segment of a circle?


In the above picture, we take a circle in which a minor sector (AOB) is shown.

Because it has less area or less angle so we are considering it as the minor sector.

Given-
The angle of the sector(AOB)=80º
Radius of circle=5cm

Put all the values in the formula-

Area of sector = (θ/360º)×Ï€r²

  • (θ/360º)Ï€r²
  • (80º/360º)(22/7)×(5)²
  • (1/4.5)(22/7)×25
  • (22/31.5)×25
  • (22×25)/31.5
  • 17.46 cm²
We get the area of minor sector 17.46 cm².


How to find the area of Segment?

Here the same, for finding the area of the segment we have a formula-

Area of segment = r²{πθ/360º-(sin(θ/2)cos(θ/2)}

This formula works when we know the values of sin & cos.
Where
  • θ= Angle of the segment
  • r= Radius of circle
  • Ï€=22/7 or 3.14

For better understanding, we take an example. Let's discuss-

Question

Find the area of the segment with radius 5 cm & if the angle of the segment is 90º.

Answer

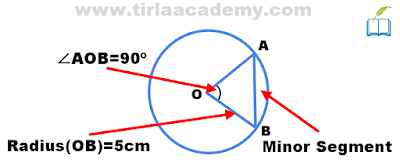
First, we draw an image for better understanding.

How to find the area of sector & segment of a circle?


In the above picture, we take a circle in which a minor segment is shown.

Because it has less area or less angle so we are considering it as the minor segment.

Given-
The angle of the segment=90º
Radius of circle=5cm

Put all the values in the formula-

  • Area of segment = r²{πθ/360º-(sin(θ/2)cos(θ/2)}
  • r²{πθ/360º-(sin(θ/2)cos(θ/2)}
  • 5²{(22/7)(90º/360º)-sin(90/2)×cos(90/2)}
  • 25{(22/7)(1/4)-sin45º×cos45º
  • 25{(22/7)(1/4)-(1/√2)×(1/√2)}
  • 25{(22/28)-(1/2)}
  • 25{(11/14)-(1/2)}
  • 25×0.285
  • 7.125cm²
We get the area of minor segment 7.125cm².

In this way, we may find the area of sector & segment of a circle.

THANK YOU...

Tags